Fizyka zmienia uczenie maszynowe
Uczenie maszynowe (ang. machine learning – ML) odcisnęło piętno praktycznie na każdym aspekcie naszego życia i to w bardzo krótkim czasie. Ten element sztucznej inteligencji zrewolucjonizował nie tylko handel i e-commerce odcisnęło piętno zastosowanie elementów sztucznej inteligencji uczenie maszynowe w większym lub mniejszym stopniu Nie ma chyba już aspektów życia w którym uczenie maszynowe nie odcisnęłoby swojego piętna.
Modele naukowe a życie
Każdy model fizyczny ma za zadanie jak najbardziej wiernie opisać rzeczywistą sytuację lub proces. Dotyczy to zresztą wszystkich modeli naukowych od fizyki przez chemię i biologię po ekonomię i socjologię. Modele bazując na odkrytych prawach naturalnych i teoriach biorą pod uwagę wiele zmiennych, które opisują realne sytuacje i procesy, wiążąc je z pomocą równań matematycznych. Przedstawiony poniżej graficznie model The General Lake Model pokazuje na przykładzie jeziora jak bardzo są skomplikowane problemy, ile zmiennych musi zostać uwzględnionych.
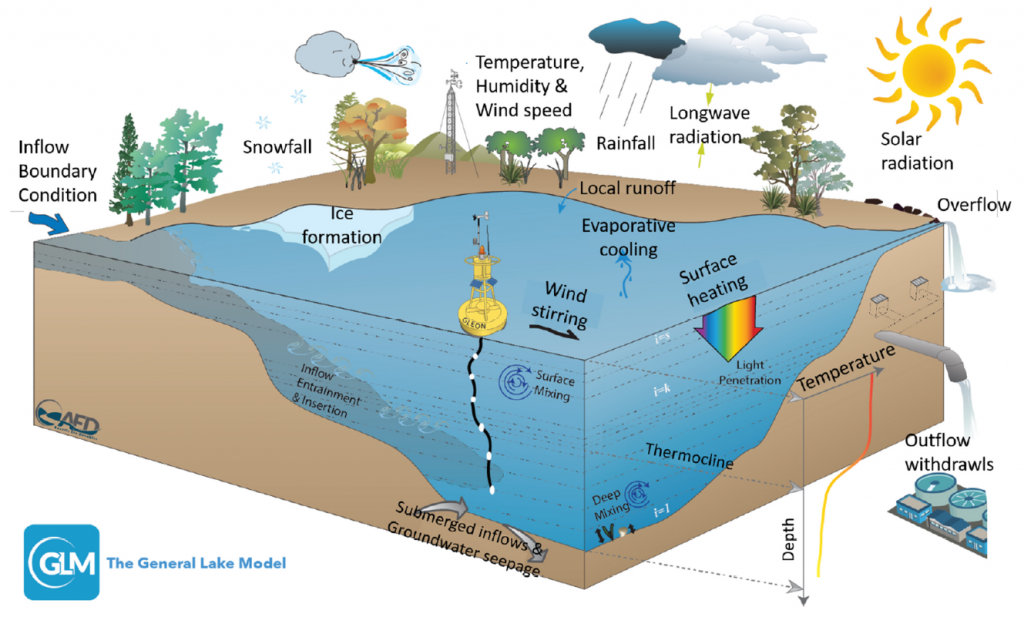
źródło: Physics-Guided Machine Learning for Scientific Discovery: An Application in Simulating Lake Temperature Profiles
Dzięki równaniom matematycznym można zasymulować w komputerze realne procesy i zbadać jak się one zachowają w innych warunkach, innym otoczeniu. Modele pozwalają uogólnić rozwiązanie konkretnego problemu na inne podobne, a nawet przez analogię zastosować w zupełnie innych dziedzinach. Nie potrzeba jest wielu danych rzeczywistych, by tą rzeczywistość odwzorować.

Niestety modele naukowe mają swoje duże ograniczenia. Nawet w zjawiskach dobrze zbadanych jest do uwzględnienia bardzo wiele zmiennych, a to powoduje dużą komplikację równań matematycznych. Najczęściej są to układy równań różniczkowych cząstkowych, a ich rozwiązanie analityczne jest możliwe tylko w bardzo nielicznych i prostych przypadkach. Dlatego konieczne są bardzo silne komputery, które są wstanie numerycznie rozwiązać te równania. Jest to jednak bardzo kosztowne, długotrwałe (tygodnie, nieraz miesiące), a często wręcz niemożliwe w skończonym czasie. Upraszczanie modeli, by je obliczyć powoduje duże niedokładności i błędy w wynikach, co może skutkować poważnymi konsekwencjami.
Równania różniczkowe powstały w wyniku prac nad opisem zagadnień fizycznych takich jak drgania, akustyka, czy hydromechanika już w XVIII wieku. Matematycznie są to zwykłe równania algebraiczne, tyle że obok prostych zmiennych i stałych zawierają operatory różniczkowe. Operatory te odwzorowują działanie sił w czasie i w przestrzeni. Pisząc w dużym skrócie zamieniają funkcje matematyczne na ich pochodne. Dla zobrazowania skomplikowania zagadnienia podam dwa proste przykłady: równanie Laplace’a i równanie Hamiltona z operatorami.
Operator Laplace’a – laplasjan zdefiniowany w układzie kartezjańskim:
$$ \bigtriangleup \equiv \nabla^2 = \frac{\partial^2}{\partial^2 x} + \frac{\partial^2}{\partial^2 y} + \frac{\partial^2}{\partial^2 z} $$Równanie różniczkowe Laplace’a:
$$ \bigtriangleup u(x) = 0 $$Równoważny zapis równania z użyciem pochodnych cząstkowych drugiego rzędu w układzie kartezjańskim:
$$ \frac{\partial^2}{\partial^2 x} u(x,y,z) + \frac{\partial^2}{\partial^2 y} u(x,y,z) + \frac{\partial^2}{\partial^2 z} u(x,y,z) = 0 $$H – Operator Hamiltona – hamiltonian dla cząstki w polu potencjalnym:
$$ \hat{H} = – \frac{\hbar^2}{2 m} \nabla^2 + V(\vec{r},t) $$Równanie Schrödingera w notacji „braketowej” i jego zapis z użyciem laplasjanu:
$$ \hat{H} | \Psi(t) \rangle = i\hbar \frac{\partial}{\partial t} | \Psi(t) \rangle $$ $$ [- \frac{\hbar^2}{2 m} \nabla^2 + V(\vec{r},t)] \ \psi(\vec{r},t) = i\hbar \frac{\partial}{\partial t} \ \psi(\vec{r},t) $$Jak można zauważyć operatory mogą być dużo bardziej skomplikowane niż tylko sama pochodna funkcji.
Nawet jeśli czegoś nie potrafimy zrozumieć, to potrafimy to zmierzyć.
Podobny problem z teoretycznymi modelami jest w przypadku procesów nie do końca poznanych lub całkowicie nie rozumianych. Jeśli czegoś nie potrafimy zrozumieć, to i opisać równaniami, choć potrafimy to nierzadko bardzo dobrze zmierzyć.
Uczenie maszynowe zmienia fizykę, czyli trafiła kosa na kamień

Właśnie wspomniana możliwość obserwowania i zmierzenia czegoś, mimo braku pełnego zrozumienia istoty rzeczy, zawsze była narzędziem naszej ludzkiej ciekawości, prowadzącej nas do odkrywania praw rządzących światem. Limitują nas tylko nasze biologiczne ograniczenia, a komputery i uczenie maszynowe pomagają nam je przesuwać.
Dlatego ogromna skala sukcesu jakie zanotowało uczenie maszynowe w zastosowaniach komercyjnych (rozpoznawanie obrazu, przetwarzanie tekstów i języka mówionego, etc.) sprawiła, że fizykom metody te wydały się bardzo obiecujące. Szybko się jednak stało oczywistym, że proste przełożenie tych samych technik do rozwiązywania modeli naukowych nie spełni pokładanych w nich nadziei. To co było do tej pory siłą metod uczenia maszynowego w e-commerce i mediach, okazało się być słabością w rozwiązywaniu modeli naukowych.
Przy wielu zmiennych
klasyczne uczenie maszynowe sobie nie radzi
Podobnie jak teoretyczne modele naukowe, klasyczne modele uczenia maszynowego oparte na drzewach decyzyjnych czy różnych metrykach odległości nie były wstanie poradzić sobie z dużą ilością zmiennych jakie występowały w modelach fizycznych. Rozwiązaniem stało się tzw. głębokie uczenie (ang. deep learning), gdzie wiele tzw. „ukrytych” warstw sieci neuronowych może wielokrotnie przetwarzać dane nim ostatecznie zostaną ustalone wartości, co pozwoliło na przetwarzanie teoretycznie nieograniczonej liczby zmiennych.
Brak danych
Modele naukowe nie potrzebują zbyt wielu danych, by dać rozwiązanie – wszystko określa teoria. Natomiast brak danych jest przeszkodą w korzystaniu z uczenia maszynowego. Modele, szczególnie te wykorzystujące głębokie uczenie, potrzebują ich bezliku. Problem w tym, że przy rozwiązywaniu problemów naukowych zwykle tych danych nie ma w wystarczającej ilości i algorytmy nie są wstanie nic sensownego przewidzieć.
Brak ogólności rozwiązania
Istotą modelu naukowego jest możliwość jego prostego uogólnienia i przełożenia na inne dziedziny. Modele te rozwiązują problem matematycznie bazując na prawach natury, parametrach początkowych oraz warunkach brzegowych. Zmieniając parametry jesteśmy wstanie otrzymać poprawny wynik dla każdej sytuacji jaką będziemy chcieli zasymulować i ewoluować go w czasie.
Rezultatem metody głębokiego uczenia jest wynik na podstawie danych wejściowych. Określają one dokładnie wiele zmierzonych sytuacji, ale nie mówią nic o innych możliwych stanach, w których środowisko może się znajdować. Takiego wyniku nie da się uogólnić i zastosować do innych zagadnień.
Długi czas uczenia maszyn
Głębokie uczenie maszyn oparte na Big Data jest bardzo czaso- i energochłonne. Czas jaki potrzebny jest do wyszkolenia modeli liczony jest nie w godzinach, a w dniach lub tygodniach. Brak ogólności rozwiązania powoduje, że dla każdego nowego zestawu danych cały wysiłek uczenia maszyn musi zostać powtórzony.
Brak przejrzystości i zrozumienia
Rozwiązywanie modeli naukowych prowadzi do zrozumienia świata i opisywania kolejnych praw nim rządzących. Rozumiemy dokładnie co się dzieje w rzeczywistości, co jest przyczyną, a co skutkiem. O ile wyniki klasycznych metody uczenia maszynowego można łatwo wytłumaczyć śledząc proces i wyniki pośrednie, o tyle głębokie sieci neuronowe są jak czarna skrzynka. Wprowadzamy dane i otrzymujemy wynik, ale nie mamy pojęcia dlaczego ten wynik jest taki a nie inny. To nie wzbogaca ani naszej wiedzy o świecie, ani nie popycha ludzkości do kolejnych odkryć.
Brak spójności z prawami fizyki
Uczenie maszynowe nie zna i nie stosuje praw fizyki
Nie każdy poprawny wynik modelu uczenia maszynowego będzie miał odzwierciedlenie w rzeczywistym świecie. Uczenie maszynowe nie zna i nie stosuje praw fizyki. Na podstawie dostarczonych danych maszyna może budować wzorce niezgodne z naszymi obserwacjami przyrody, a ponieważ modele naukowe rozwiązują zdecydowanie bardziej krytyczne zadania niż rekomendacje produktów, to może prowadzić do poważnych konsekwencji dla zdrowia i życia ludzi.

Uczenie maszynowe oparte na wiedzy
Mimo barier uczeni nie porzucili jednak technik uczenia maszynowego, ponieważ profity wynikające ze znacznego przyspieszenia rozwiązywania modeli oraz możliwość badania i symulowania nie do końca poznanych procesów dają szanse na szybsze kolejne przełomy w nauce.
Modele fizyczne jako pierwsze zostały poddane próbie wykorzystania głębokiego uczenia. Wszystkie problemy z zastosowaniem tej metody w sposób jaki była do tej pory używana, wynikają z tego, że uczenie to nie ma pojęcia o prawach fizycznych rządzących światem. Dlatego naukowcy postanowili nauczyć maszyny tych zasad, wprowadzając ograniczenia wynikające z natury badanego zagadnienia. Jednocześnie okazało się, że nowe podejście oparte na wiedzy jest przydatne w szczególności dla rozwoju głębokiego uczenia na sieciach neuronowych w dotychczasowych ich zastosowaniach.
Koncepcja włączenia dodatkowych reguł w sieci neuronowe, których źródłem jest nie tylko fizyka, pojawia się pod różnymi angielskimi nazwami, np.: physics guided machine learning – PGML, physics inspired neural networks – PINN, czy physics aware artificial intelligence, a także bardziej ogólnymi: knowledge guided machine learning – KGML czy scientific machine learning.
Zainteresowanie nowym podejściem do uczenia maszynowego gwałtownie rośnie, coraz więcej badań się prowadzi i powstaje coraz więcej prac naukowych. Widać to zarówno po liczbie pojawiających się publikacji jak i częstości wyszukiwanych fraz z tym związanych.
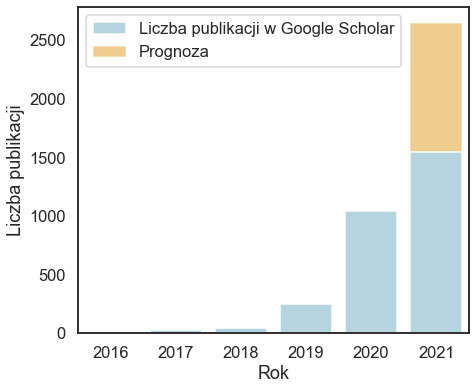
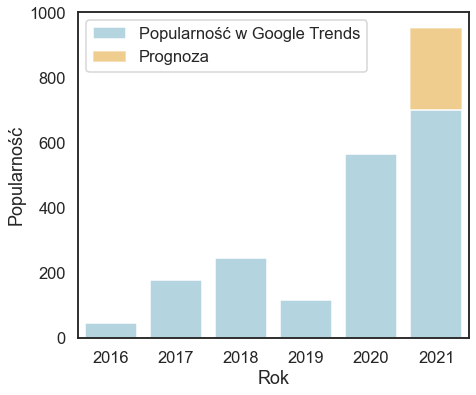
Czym tak naprawdę jest omawiana zmiana w podejściu do uczenia maszynowego? Nie ma jednego przepisu, reguły, według której należało by postępować. Jest to zbiór pomysłów, który ciągle jest wzbogacany i rozwijany dzięki kolejnym doświadczeniom i pracom naukowym.
Rozwiązanie równań różniczkowych zamiast uczenia konkretnego modelu
Równania różniczkowe cząstkowe są sercem modelu naukowego, to one opisują rzeczywistość odwzorowując w ten sposób oddziaływanie wielu sił na wiele obiektów i równocześnie zmiany w czasie. Równań tych w modelu jest tak wiele i są tak skomplikowane, że prawie zawsze można je rozwiązać wyłącznie numerycznie, co wymaga nawet wielu tygodni, czy miesięcy obliczeń na superkomputerach.
Próbując rozwiązać model naukowy w tradycyjny sposób dla uczenia maszynowego fizycy natknęli się cały szereg wspomnianych już problemów: za mało realnych danych do nauczenia maszyn, artefakty w wynikach nie dające się wytłumaczyć prawami fizyki, konieczność ponownego uczenia maszyn jeśli tylko zmieniły się dane wejściowe i oczywiście niemożność przeniesienia rozwiązania na inne analogiczne zagadnienia, np. z mechaniki płynów na ruch samochodowy.
Z pomocą przyszły sieci neuronowe, które pozwalają przybliżyć dowolną funkcję ciągłą na podstawie uniwersalnego twierdzenia aproksymacyjnego. Dodanie jednej ukrytej warstwy spowodowało, że nie tylko funkcje, ale i nieliniowe operatory różniczkowe można przybliżać. Pierwszą architekturą pozwalającą na to była sieć DeepONet (Lu Lu, Pengzhan Jin, George Em Karniadakis). O tym jak wygląda rozwiązywanie równań możecie przeczytać w tym artykule – Rozwiązywanie równań różniczkowych cząstkowych za pomocą głębokiego uczenia.
Bazując na tym samym pomyśle powstała też sieć FNO – Fourier Neural Operator (Zongyi Li, Nikola Kovachki, Kamyar Azizzadenesheli, Burigede Liu, Kaushik Bhattacharya, Andrew Stuart, Anima Anandkumar) używająca popularnej w rozwiązywaniu zagadnień fizycznych transformaty Fouriera. Dzięki temu jest możliwość obliczenia nie tyle bezpośrednio samego modelu na sieci neuronowej, co wielokrotne przyspieszenie obliczeń numerycznych pozostawiając go nadal modelem naukowych wraz z możliwością uogólnienia rozwiązania i zastosowania go w innych dziedzinach.
Funkcja kosztu oparta na wiedzy
Funkcja kosztu (straty) jest kluczowa dla uczenia maszynowego. Reprezentuje ona karę za niedokładność prognozy wartości zmiennych. Jej minimalizacja w kolejnych krokach algorytmu prowadzi do znalezienia optymalnego rozwiązania. Jak już wspomniałem ze względu na wzajemne relacje wielu zmiennych zmieniających się w czasie i przestrzeni, standardowe modele uczenia maszynowego nie są wstanie na podstawie danych wywnioskować zależności, zwłaszcza przy ograniczonych ilościach obserwacji. Skutkuje to również znajdowaniem rozwiązań nie mających odzwierciedlenia w rzeczywistości mimo, iż sam nauczony model z punktu widzenia błędów statystycznych ma bardzo dobrą trafność prognoz. Rezultatem jest też brak możliwości uogólnienia na scenariusze, które nie są reprezentowane w danych. Takiego modelu nie da się też odpowiednio dobrze wyjaśnić, skąd się wzięło takie rozwiązanie, zwłaszcza przy głębokim uczeniu.
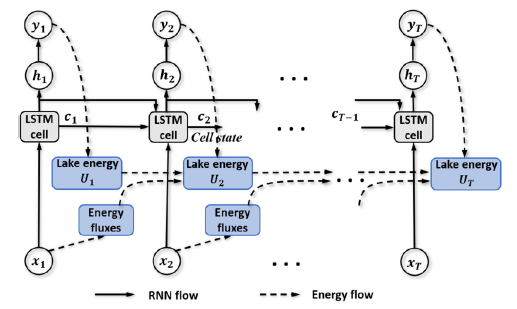
(Physics-Guided Machine Learning for Scientific Discovery: An Application in Simulating Lake Temperature Profiles)
Dlatego naukowcy dodają do funkcji kosztu wiedzę fizyczną, aby modele uczenia maszynowego były wstanie odnaleźć wzorce zgodne ze znanymi prawami fizycznymi. Najczęściej dodaje się ograniczenia wynikające z tych praw, np. zasadę zachowania energii. Pozwala to nie tylko poprawić prognozowanie na podstawie tak nauczonego modelu, ale też zawęzić pole poszukiwań do rozwiązań spójnych naukowo. Zawężenie pola poszukiwań może skrócić też czas potrzebny do wytrenowania maszyny.
Inicjalizacja parametrów za pomocą wiedzy
Modele uczenia maszynowego do rozpoczęcia procesu trenowania zwykle wymagają określenia parametrów początkowych, które mogą być dobrane na wiele różnych sposobów, również w sposób losowy zgodnie z wybranym rozkładem. Źle dobrane parametry mogą spowodować, że model podczas trenowania znajdzie się w lokalnym minimum i algorytm nie będzie potrafił z niego się wydostać. Dlatego dobranie parametrów na podstawie wiedzy o badanym zjawisku pozwala na ucieczkę z lokalnych minimów a także zmniejszenie ilości danych do trenowania, a w konsekwencji przyspieszenie uczenia i otrzymania lepszego modelu.
Często w uczeniu maszynowym stosuje się modele wstępnie wyuczone na szerokiej populacji danych, dzięki czemu można już docelowe modele szkolić na zawężonych danych treningowych i dopasować je do szczegółowego zagadnienia. Wstępnie wytrenowany model określa zatem stan początkowy bardziej zbliżony do poszukiwanego rozwiązania niż losowy dobór parametrów.
Stosując symulacje komputerowe oparte na posiadanej wiedzy można dostarczyć dane do wstępnego przeszkolenia sieci neuronowych. Tak wstępnie wyuczony model będzie miał lepszą skuteczność i wyniki mające większy sens fizyczny. Jest to też bardzo ważne z punktu widzenia badania zjawisk nie do końca jeszcze poznanych. W ten sposób mając ograniczoną wiedzę ale i dane można zbudować model, który pozwoli szybciej i lepiej takie zjawiska odkrywać.
Architektura uczenia maszynowego oparta na fizyce
Pojęcie architektury odnosi się przede wszystkim do sieci neuronowych. Dzięki ich elastyczności i modularnej budowie można je kształtować i dostosowywać do potrzeb.
Zmienne fizyczne w sieci neuronowej
W sieciach neuronowych można przypisać wybranym neuronom fizyczne zmienne, jak np. temperatura wraz z ograniczeniami wynikającymi z praw fizyki. Znając więc zagadnienie od strony naukowej można podczas szkolenia modeli weryfikować dane pośrednie, czy mieszczą się one w założonych granicach. W ten sposób model jest bardziej odporny na nauczenie się fałszywych wzorców a sam czas trenowania krótszy. Pozwala to też na wydobycie z czarnoskrzynkowych modeli jakimi są sieci neuronowe informacji, które mogą być zinterpretowane przez ekspertów z danej dziedziny. Dzięki temu można rozwiązać wielki problem jakim jest brak możliwości dobrego objaśnienia działania modelu.
CAN – sieci neuronowe, które mówią – „nie wiem”
W uczeniu maszynowym przyzwyczajeni jesteśmy, że zawsze otrzymujemy odpowiedź na nasze pytanie, co najwyżej jej nie ufamy, bo prawdopodobieństwo jej prawdziwości jest nikłe. Granica tej ufności jest przy tym dość płynna i zależy od kontekstu. Nie zawsze jest to jednak najlepsze podejście. Czasami chcemy i musimy wiedzieć, że nie można dostać poprawnej odpowiedzi, bo danych jest za mało, np. w prognozach klimatycznych. Dlatego powstały sieci CAN – ang. Controlled Abstention Networks, które potrafią powiedzieć „nie wiem”.
Symetrie i niezmienniczość przekształceń
W modelach fizycznych bardzo ważną rolę spełniają symetrie i przekształcenia niezmiennicze, które wiążą systemy i ich dynamikę z symetriami. Słynne twierdzenie Noether wiąże zasady zachowania pędu, energii, czy ładunku z symetriami. Obecne architektury sieci neuronowych RNN i CNN implementują już niektóre symetrie i przekształcenia. Realizacja praw wynikających z symetrii i niezmienniczości sprawia, że otrzymany model jest bardziej zgodny z rzeczywistością, bardziej wiarygodny i możliwy do uogólnienia na inne scenariusze. Zmniejsza się też przestrzeń, w której należy szukać rozwiązań, co pomaga ograniczyć nakłady i czas na uczenie modeli.
Zastosowanie praw fizyki związanych z symetrią i przekształceniami niezmienniczymi zmienia też tradycyjne konwolucyjne sieci neuronowe wykorzystywane przy rozpoznawaniu obrazów. Na skutek braków danych obrazy będące zbiorem uczącym muszą być wzbogacone o swoje transformacje, jak obroty, odbicia, czy zaszumienia. Sama operacja zwana augmentacją nie tylko wydłuża czas przygotowania danych, ale przede wszystkim czas samego uczenia – trzeba więcej obrazów wysłać do sieci neuronowej. Rozwiązaniem jest wprowadzenie tych przekształceń już do samej sieci, która w naturalny dla siebie sposób dokonuje transformacji. Jest to znacznie szybsze i pozwala zaoszczędzić nie tylko czas, ale zasoby i zużywaną energię elektryczną.
Modele hybrydowe
Ponieważ modele naukowe i uczenia maszynowego różnią się sposobami rozwiązania problemów stosuje się też hybrydowe modele, gdzie oba podejścia pracują symultanicznie lub elementy w modelu naukowym są zastępowane przez modele uczenia maszynowego. Wykorzystuję się tu regresję liniową do predykcji wartości zmiennych fizycznych. Innym podejściem jest zastosowanie wyników działania modeli naukowych jako parametrów wejściowych do modeli uczenia maszynowego. W przypadku pewnych braków i niedoskonałości modeli naukowych stosuje się modele uczenia maszynowego zastępując nimi część modelu naukowego.
Podsumowanie
Uczenie maszynowe, a zwłaszcza głębokie uczenie na sieciach neuronowych osiągnęło błyskawiczny sukces w zastosowaniach komercyjnych, szczególnie przy przetwarzaniu obrazów, języka naturalnego, czy dźwięków. Jednak konfrontacja z modelami naukowymi wymusza rozwój tej dziedziny w zupełnie nowym kierunku. Już nie tylko same dane, ale także prawa fizycznie, a ogólnie mówiąc nasza wiedza o prawach natury są źródłem zachowania się algorytmów. Nowe podejście powoduje też większy nacisk na rozwój teorii matematycznych opisujących głębokie uczenie.
Nowe podejście do uczenia maszynowego może rozwiązać wiele problemów również w obszarach, gdzie jest święci ono już tryumfy. Możemy poprawić skuteczność algorytmów, skrócić czas uczenia, rozszerzyć stosowalność na przypadki z ograniczoną liczbą danych, pogłębić uniwersalność rozwiązań i w pełni zrozumieć informację z wnętrza czarnej skrzynki jaką jest głębokie uczenie, a także poprawić efektywność energetyczną infrastruktury przez ograniczenie zużycia prądu i materiałów.
Uczenie maszynowe oparte na wiedzy to dla mnie kolejny duży krok w dziedzinie szeroko pojętej sztucznej inteligencji. W niedalekiej przyszłości dzięki inkorporacji wiedzy do algorytmów modele uczenia maszynowego będą miały bardzo duży wpływ na każdą dziedzinę naszego życia i to w najdrobniejszych jego aspektach.
Bibliografia
- Integrating Scientific Knowledge with Machine Learning for Engineering and Environmental Systems
- Harnessing the Data Revolution: Knowledge Guided Machine Learning – A Framework for Accelerating Scientific Discovery
- Physics-Guided Machine Learning for Scientific Discovery: An Application in Simulating Lake Temperature Profiles
- DeepONet: Learning nonlinear operators for identifying differential equations based on the universal approximation theorem of operators
- Fourier Neural Operator for Parametric Partial Differential Equations
- Implementacja FNO – Fourier Neural Operator na github (python, PyTorch)
- Physics Informed Neural Network for Time-Dependent Nonlinear and Higher Order Partial Differential Equations
- Physics-informed graph neural Galerkin networks: A unified framework for solving PDE-governed forward and inverse problems
- Physics Informed by Deep Learning: Numerical Solutions of Modified Korteweg-de Vries Equation
- Controlled abstention neural networks (CAN) for identifying skillful predictions for regression problems
- Geometric Deep Learning: Grids, Groups, Graphs, Geodesics, and Gauges