
Rozwiązywanie równań różniczkowych cząstkowych za pomocą głębokiego uczenia
Równania różniczkowe cząstkowe są jednym z podstawowych narzędzi matematycznych do opisu rzeczywistego układu i zachodzących w nim zmian w czasie. Stosuje się je począwszy od fizyki, gdzie wzięły swój początek, przez chemię, biologię, aż po socjologię i ekonomię.
Niestety dla większości opisywanych zjawisk tworzą one skomplikowane układy równań. Ich rozwiązanie analityczne jest możliwe tylko w bardzo niewielu przypadkach. Ogromną większość można rozwiązać tylko numerycznie na bardzo silnych komputerach, a i tak zajmuje to bardzo dużo czasu: dni, tygodnie, a nawet miesiące.
Próby wykorzystania sieci neuronowych i głębokiego uczenia bezpośrednio do modelowania natury na podstawie danych natrafiły na bardzo poważne problemy, o czym możecie przeczytać w osobnym artykule – Fizyka zmienia uczenie maszynowe. Na szczęście te narzędzia uczenia maszynowego fizycy byli wstanie wykorzystać w zupełnie nowy sposób.
DeepONet
Dzięki uniwersalnej teorii aproksymacji z teorii sieci neuronowych udało się przybliżać nie tylko ciągłe funkcje matematyczne, ale i nieliniowe operatory różniczkowe.
Zespół naukowców Lu Lu, Pengzhan Jin i George Em Karniadakis z Chińskiej Akademii Nauk oraz Uniwersytetu Brown w Providence w USA stworzył architekturę sieci neuronowych do aproksymacji operatorów różniczkowych o nazwie DeepONet – deep operator networks.
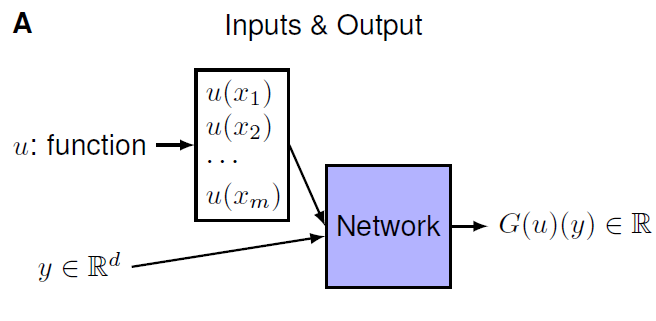
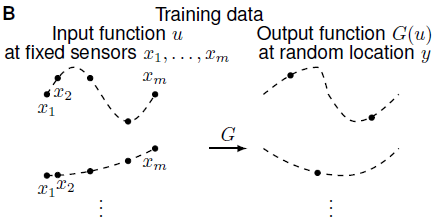
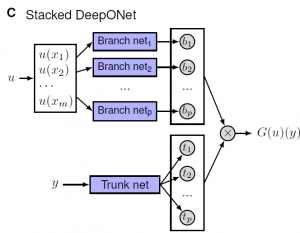
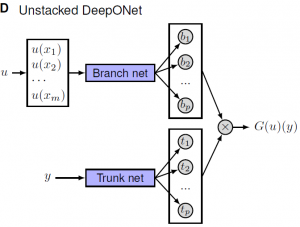
Celem jest nauczenie sieci neuronowej przybliżania operatora $G$ (oznaczenie za autorami) działającego na funkcje $u(x)$. Sieć DeepONet jest zbudowana z dwóch podsieci neuronowych i przyjmuje na wejściu dwa zestawy danych. Jedna podsieć jest odpowiedzialna za przybliżanie wartości funkcji $u(x)$ ze stałej listy sensorów w punktach $\{x_1, x_2, x_3, … , x_n\}.$ Druga podsieć ma zadanie lokalizować wynik działania operatora $G(u)$. Rezultatem jest złożenie tych dwóch wyników razem.
 |  |
Po szczegóły naukowe i techniczne odsyłam do pracy naukowej „DeepONet: Learning nonlinear operators for identifying differentia equations based on the universal approximation theorem of operators”.
Równania różniczkowe w Python

Jako przykład zastosowania wybrałem równanie Burgersa, które jest jednym z podstawowych równań w mechanice płynów, zajmującą się zachowaniem płynów, gazów oraz wywieranych przez nie siłach. Dzięki mechanice płynów konstruuje się napęd odrzutowy, turbiny wiatrowe czy hamulce hydrauliczne, a nawet projektuje zastawki mechaniczne serca. Równanie Burgersa zastosowanie znalazło również w modelach dynamiki ruchu ulicznego. Wykorzystuje się je także w meteorologii do przewidywania ruchu atmosfery wirującej wokół Ziemi przy prognozowaniu pogody.

Równanie Burgersa służy także do modelowania ruchu ulicznego
Równanie Burgersa wiąże prędkość płynu $u$ z położeniem $x$ i czasem $t$ oraz lepkością płynu $\nu$. Człon po prawej stronie równania opisuje dyssypację, czyli rozpraszanie energii. W ruchu ulicznym lepkość odwzorowuje zachowania kierowców, mających różny czas reakcji przy ruszaniu i hamowaniu, czy zmianie pasa ruchu.
$$ \frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} = \nu \frac{\partial^2 u}{\partial x^2} $$gdzie $x$ – położenie, $t$ – czas, $u$ – prędkość płynu, $\nu$ – stała lepkości.
Jeśli pominiemy lepkość, to równanie upraszcza się do nielepkiego równania Burgersa:
$$ \frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} = 0 $$Dla porównania zbadamy również niejednorodne lepkie równanie Burgersa, które posiada dodatkowy człon z funkcją nieróżniczkowalną $F(x,t)$. Niejednorodność pozwala odwzorować wpływ właściwości środowiska, w którym modelujemy zjawisko.
$$
\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} = \nu \frac{\partial^2 u}{\partial x^2} + F(x,t)
$$
Biblioteka DeepXDE
Autorzy architektury DeepONet stworzyli bibliotekę DeepXDE dla języka Python, która w przystępny sposób pozwala na wykorzystanie tej specjalnej sieci neuronowej do rozwiązywania równań różniczkowych.
Instalacja DeepXDE przez PyPi:
pip install deepxdeInstalacja DeepXDE przez Conda:
conda install -c conda-forge deepxdeDo budowy sieci neuronowych wykorzystuje ona biblioteki TensorFlow (instalacja) lub PyTorch (instalacja). Ma dość dobrze opisany interfejs oraz przykłady dla różnych zagadnień wraz z danymi testowymi (obliczenia analityczne lub numeryczne równań). W poniższym przykładzie wybrałem bibliotekę PyTorch jako podstawę dla budowy sieci neuronowych przez DeepXDE.
Import koniecznych bibliotek:
import numpy as np
import deepxde as dde
import torch
from scipy.stats import normNielepkie równanie Burgersa
Przykład zaczniemy od najprostszej nielepkiej postaci równania Burgersa, które jak już wiemy ma następująca postać:
$$
\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} = 0
$$
Definicja przestrzeni i czasu
Potrzebujemy zdefiniować geometrię czasoprzestrzenną, w której to będziemy modelować zachowanie się układu. Dla uproszczenia będzie to model jednowymiarowy, ale dzięki temu na wykresie 3D będzie można zobaczyć ewolucję w czasie.
Położenie będzie w zakresie $x \in [-1,1]$ , natomiast czas $t \in [0,1]$ :
geom = dde.geometry.Interval(-1, 1)
timedomain = dde.geometry.TimeDomain(0, 1)
geomtime = dde.geometry.GeometryXTime(geom, timedomain)Definicja równania różniczkowego
W równaniu występuje pochodna cząstkowa prędkości płynu pierwszego rzędu po czasie oraz pochodna cząstkowa pierwszego rzędu po położeniu. Reprezentacją pochodnych cząstkowych dla wspomnianej listy sensorów jest macierz Jacobiego zwana jakobianem. Choć biblioteki PyTorch i TensorFlow mają swoje definicje jakobianów, to autorzy polecają stosować wersję „lazy” z DeepXDE, która wylicza elementy macierzy tylko wtedy, gdy jest to konieczne i dodatkowo zapamiętuje wyniki.
Funkcja pde definiująca równanie różniczkowe ma dwa argumenty. Pierwszym jest dwuwymiarowy wektor czasoprzestrzenny $x$, który zawiera położenie $x[:0]$ i czas $x[:1]$ (odpowiednio zmienna $j=0, j=1$), który jest daną wejściową dla sieci. Drugim jest funkcja prędkości $u(x,t)$, która jest wynikiem działania sieci.
def pde(x, u):
du_x = dde.grad.jacobian(u, x, i=0, j=0)
du_t = dde.grad.jacobian(u, x, i=0, j=1)
return du_t + u * du_xWarunki brzegowe i początkowe
Warunki brzegowe określają jak funkcja ma się zachowywać na brzegu określonego wcześniej obszaru. W mechanice płynów, czyli w niniejszym przykładzie często przyjmuje się, że cząsteczki płynu nie poruszają się. Dlatego zastosowano tu warunek brzegowy Dirichleta i dla zmiennej położenia $x = 0$.
bc = dde.DirichletBC(geomtime, lambda x: 0, lambda _, on_boundary: on_boundary)Model musi mieć też określony swój stan początkowy, czyli w chwili $t = 0$. W tym przykładzie dane dla położenia zostały wygenerowane za pomocą rozkładu normalnego.
ic = dde.IC(
geomtime,
lambda x: norm.pdf(x[:,0:1],0.0,0.2).reshape(-1,1),
lambda _, on_initial: on_initial
)Budowa i trenowanie sieci neuronowej z głębokim uczeniem
Gdy mamy już określoną dziedzinę (czasoprzestrzeń), równanie różniczkowe i warunki brzegowe oraz początkowe, to można zbudować rozwiązanie zależne od czasu, w którym określamy odpowiednio liczbę punktów do trenowania sieci próbkowanych w dziedzinie, liczbę punktów do próbkowania na brzegu oraz dodatkowo dla warunków początkowych.
data = dde.data.TimePDE(
geomtime, pde, [bc, ic], num_domain=2540, num_boundary=80, num_initial=320
)Następnie wybieramy sieć FNN (ang. fully-connected neural network) i w definicji sieci podajemy ile ukrytych warstw neuronów (4) i jak mają być szerokie (20), a także wybieramy funkcję aktywatora $tanh$ i inicjator sieci „Glorot normal”.
net = dde.maps.FNN([2] + [20] * 4 + [1], "tanh", "Glorot normal")W ten sposób definiujemy model podając mu zdefiniowane wcześniej rozwiązanie oraz sieć neuronową, optymalizator (Adam) i współczynnik szybkości uczenia się (ang. learning rate, $lr=1e-3$). Po 15 tys. iteracji, w których to model się uczył możemy zmienić optymalizator by osiągnąć lepszą dokładność w kolejnych krokach (L-BFGS).
model = dde.Model(data, net)
model.compile("adam", lr=1e-3)
model.train(epochs=15000)
model.compile("L-BFGS")
losshistory, train_state = model.train()Równanie Burgersa (lepkie)
W równaniu uwzględniającym lepkość środowiska mamy dodatkowy człon z drugą pochodną prędkości po położeniu i stałym współczynnikiem lepkości odpowiadający za rozpraszanie energii.
$$
\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} = \nu \frac{\partial^2 u}{\partial x^2}
$$
Aby uwzględnić wpływ lepkości wystarczy dodać do definicji funkcji pde macierz Hessego zwaną hesjanem, która reprezentuje właśnie różniczkę drugiego rzędu oraz wybrać współczynnik lepkości – np. $\nu = 0.5$.
def pde(x, y):
dy_x = dde.grad.jacobian(y, x, i=0, j=0)
dy_t = dde.grad.jacobian(y, x, i=0, j=1)
dy_xx = dde.grad.hessian(y, x, i=0, j=0)
return dy_t + y * dy_x - 0.5 * dy_xxW wersji niejednorodnej dodajemy człon z funkcją sinus.
def pde(x, y):
dy_x = dde.grad.jacobian(y, x, i=0, j=0)
dy_t = dde.grad.jacobian(y, x, i=0, j=1)
dy_xx = dde.grad.hessian(y, x, i=0, j=0)
return dy_t + y * dy_x - 0.5 * dy_xx - 5 * torch.sin(x[:, 0:1])Poniżej pełny kod skryptu wraz z dodatkową funkcją plot_3d do wizualizacji ewolucji w czasie (oś $t$). Ponieważ jest sporo parametrów, którymi można sterować uczenie modeli, to dla celów dydaktycznych pozostawiłem pełne funkcje bez próby wydzielania części wspólnych i innego refactoringu kodu.
import numpy as np
import deepxde as dde
import torch
from scipy.stats import norm
import matplotlib.pyplot as plt
import matplotlib
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
def plot_3d(elev, azim, train_state, colormap = cm.rainbow, figsize = (8,6)):
xs = train_state.X_train[:,0]
ys = train_state.X_train[:,1]
zs = train_state.best_y
colormap = colormap
cnorm = matplotlib.colors.Normalize(vmin=min(zs), vmax=max(zs))
scalarMap = cm.ScalarMappable(norm=cnorm, cmap=colormap)
fig = plt.figure(figsize=figsize)
ax = Axes3D(fig, auto_add_to_figure=False)
ax.view_init(elev, azim)
ax.set_xlabel('x')
ax.set_ylabel('t')
ax.set_zlabel('y')
fig.add_axes(ax)
ax.scatter(xs, ys, zs, c=scalarMap.to_rgba(zs), marker='.')
scalarMap.set_array(zs)
fig.colorbar(scalarMap)
plt.show()
def solve_inviscid_burgers_equation():
def pde(x, u):
du_x = dde.grad.jacobian(u, x, i=0, j=0)
du_t = dde.grad.jacobian(u, x, i=0, j=1)
return du_t + u * du_x
geom = dde.geometry.Interval(-1, 1)
timedomain = dde.geometry.TimeDomain(0, 1)
geomtime = dde.geometry.GeometryXTime(geom, timedomain)
bc = dde.DirichletBC(geomtime, lambda x: 0, lambda _, on_boundary: on_boundary)
ic = dde.IC(
geomtime,
lambda x: norm.pdf(x[:,0:1],0.0,0.2).reshape(-1,1),
lambda _, on_initial: on_initial
)
data = dde.data.TimePDE(
geomtime, pde, [bc, ic], num_domain=2540, num_boundary=80, num_initial=320
)
net = dde.maps.FNN([2] + [20] * 4 + [1], "tanh", "Glorot normal")
model = dde.Model(data, net)
model.compile("adam", lr=1e-3)
model.train(epochs=15000)
model.compile("L-BFGS")
losshistory, train_state = model.train()
return losshistory, train_state
def solve_viscous_burgers_equation():
def pde(x, y):
dy_x = dde.grad.jacobian(y, x, i=0, j=0)
dy_t = dde.grad.jacobian(y, x, i=0, j=1)
dy_xx = dde.grad.hessian(y, x, i=0, j=0)
return dy_t + y * dy_x - 0.5 * dy_xx
geom = dde.geometry.Interval(-1, 1)
timedomain = dde.geometry.TimeDomain(0, 1)
geomtime = dde.geometry.GeometryXTime(geom, timedomain)
bc = dde.DirichletBC(geomtime, lambda x: 0, lambda _, on_boundary: on_boundary)
ic = dde.IC(
geomtime,
lambda x: norm.pdf(x[:,0:1],0.0,0.2).reshape(-1,1),
lambda _, on_initial: on_initial
)
data = dde.data.TimePDE(
geomtime, pde, [bc, ic], num_domain=2540, num_boundary=80, num_initial=160
)
net = dde.maps.FNN([2] + [22] * 3 + [1], "tanh", "Glorot normal")
model = dde.Model(data, net)
model.compile("adam", lr=1e-3)
model.train(epochs=15000)
model.compile("L-BFGS")
losshistory, train_state = model.train()
return losshistory, train_state
def solve_nonhomogeus_viscous_burgers_equation():
def pde(x, y):
dy_x = dde.grad.jacobian(y, x, i=0, j=0)
dy_t = dde.grad.jacobian(y, x, i=0, j=1)
dy_xx = dde.grad.hessian(y, x, i=0, j=0)
return dy_t + y * dy_x - 0.5 * dy_xx - 5 * torch.sin(x[:, 0:1])
geom = dde.geometry.Interval(-1, 1)
timedomain = dde.geometry.TimeDomain(0, 0.99)
geomtime = dde.geometry.GeometryXTime(geom, timedomain)
bc = dde.DirichletBC(geomtime, lambda x: 0, lambda _, on_boundary: on_boundary)
ic = dde.IC(
geomtime,
lambda x: norm.pdf(x[:,0:1],0.0,0.2).reshape(-1,1),
lambda _, on_initial: on_initial
)
data = dde.data.TimePDE(
geomtime, pde, [bc, ic], num_domain=2540, num_boundary=80, num_initial=160
)
net = dde.maps.FNN([2] + [22] * 3 + [1], "tanh", "Glorot normal")
model = dde.Model(data, net)
model.compile("adam", lr=1e-3)
model.train(epochs=15000)
model.compile("L-BFGS")
losshistory, train_state = model.train()
return losshistory, train_state
ibe_losshistory, ibe_train_state = solve_inviscid_burgers_equation()
vbe_losshistory, vbe_train_state = solve_viscous_burgers_equation()
nh_vbe_losshistory, nh_vbe_train_state = solve_nonhomogeus_viscous_burgers_equation()
plot_3d(45,270, ibe_train_state)
plot_3d(45,270, vbe_train_state)
plot_3d(45,270, nh_vbe_train_state)
plot_3d(45,200, ibe_train_state)
plot_3d(45,200, vbe_train_state)
plot_3d(45,200, nh_vbe_train_state)
plot_3d(45,30, ibe_train_state)
plot_3d(45,30, vbe_train_state)
plot_3d(45,30, nh_vbe_train_state)Porównanie wyników
Poniżej zestawiłem wyniki jednowymiarowych ewolucji w czasie trzech wspomnianych wcześniej wersji równania Burgera. Widać na nich falę uderzeniową przemieszczającą się i z biegiem czasu (oś $t$) spłaszczającą się.
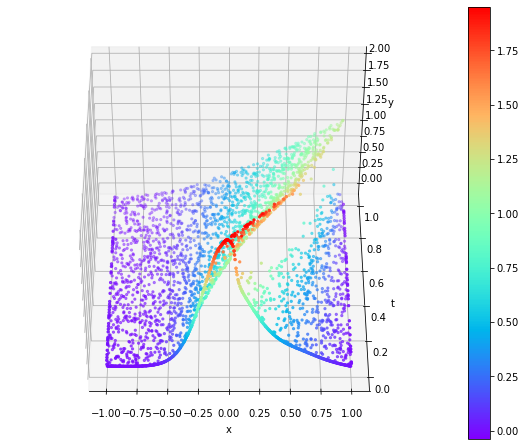 | 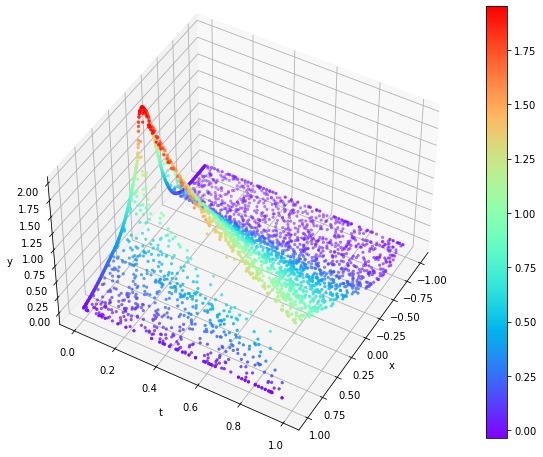 |
Po wprowadzeniu dużego czynnika lepkości i członu dyssypacji energii (pochodna drugiego rzędu) fala uderzeniowa szybko się „rozpłynęła”.
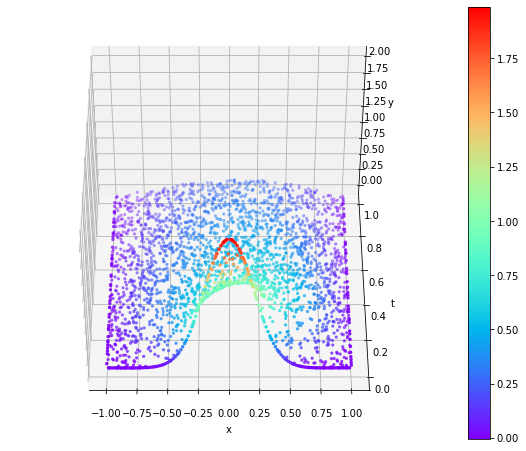 | 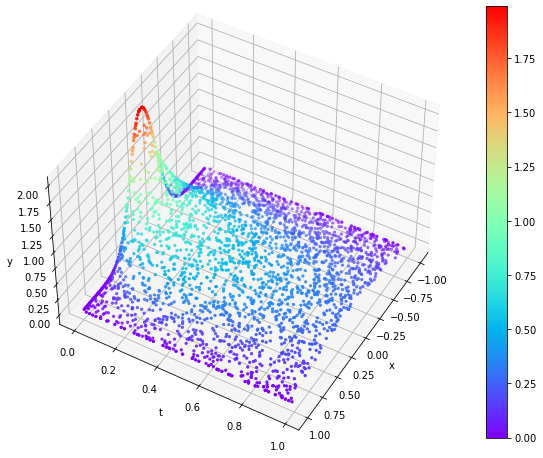 |
Wprowadzona niejednorodność do równania w postaci sinusoidy wpłynęła na bazowy kształt całego rozwiązania.
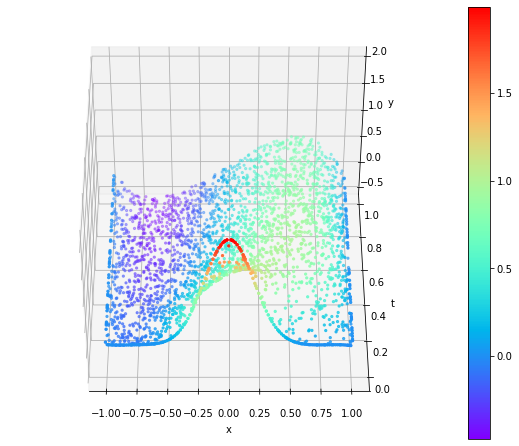 | 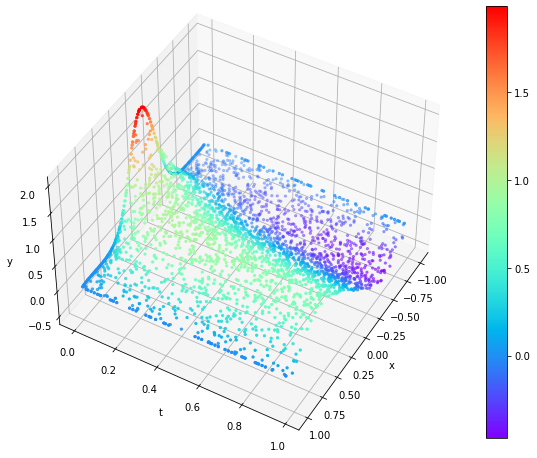 |
Testowanie i poprawność modeli
Zespół naukowców przetestował sieć DeepONet na czterech różnych problemach związanych z różniczkami zupełnymi i cząstkowymi, z których wynika, że sieć ta może dawać małe błędy aproksymacji. Przy okazji zauważono ciekawe efekty w trakcie uczenia, których do tej pory nie obserwowano w głębokich sieciach neuronowych. Nie wszystko jest też jasne z teoretycznego punktu widzenia i potrzebne są dalsze badania nad sieciami neuronowymi, by lepiej zrozumieć ich zachowanie.
Gdyby chcieć modele fizyczne opisane równaniami różniczkowymi i aproksymowane głębokimi sieciami neuronowymi w tradycyjny sposób testować, to można by zrobić to tylko jeśli istnieje rozwiązanie analityczne lub udało się je rozwiązać numerycznie. Wówczas można by bezpośrednio obliczyć błąd aproksymacji dla konkretnego modelu. Z drugiej strony przewagą modeli naukowych jest możliwość ich uogólniania na przypadki, dla których nie mamy wystarczających lub w ogóle dostępnych danych.
Bibliografia
- DeepONet: Learning nonlinear operators for identifying differential equations based on the universal approximation theorem of operators
- DeepXDE – instrukcja i przykłady
- DeepXDE – GitHub
- Regularization by noise and stochastic Burgers equations
- A physics-informed variational DeepONet for predicting the crack path in brittle materials
- Solving Partial Differential Equations Using Deep Learning and Physical Constraints
- Full Discretization of Stochastic Burgers Equation with Correlated Noise
- Diffusion approximation for self-similarity of stochastic advection in Burgers’ equation
- On the Numerical Solution of One-Dimensional Nonlinear Nonhomogeneous Burgers’ Equation
- Adam: A Method for Stochastic Optimization





